This post was originally written and posted to a Discord server shared by my friends and I on September 1st, 2022. I made minor edits between then and the current post.

Time complexity is the fundamental metric in computer science used to describe the runtime of an algorithm. If an algorithm for a given task has a lower time complexity than another for the same task, then it is provably faster for all possible inputs. The basis for time complexity lay in the growth rate of the function describing the exact runtime of the algorithm in question.

Given:

• An array of numbers, $A$. For example, $A = [ 1, 3, 2 ]$.
• An empty array, $R$.

We could write an algorithm to sort the array $A$ in order of least to greatest.

R = an empty array

while A is not empty:
	MINIMUM = first element of A
	for each number, N, in A:
		if N < MINIMUM then let MINIMUM = N
		otherwise, do nothing

	insert MINIMUM at the start of R
	remove MINIMUM from A

To fill up $R$, we have to find every minimum element of $A$. We have to check all $n$ items of $A$ to find the first minimum (all items), then $n-1$ elements (we already found a minimum), then $n-2$ (we found another), … and so on. So it takes $n * 1 = n$ time to find a minimum in the worst case scenario.

In the absolute worst case scenario, the array $A$ is in reverse order. In this situation, we have to check the entire array to find every “next minimum” element to insert into $R$. Since we need to locate $n$ elements to fill $R$, and we have to check at most $n$ items to get each of those, we say this takes $O(n^2)$ operations, which means the algorithm’s runtime is always less than some constant multiple of $n^2$. For example, $2n^2$ or $10n^2$ are all multiples of $n^2$, but since there exists some integer greater than their current multiple, they are all $O(n^2)$.

Intuitively, this might not make sense. “Well couldn’t you just say $O(n)$ is $n$ times a billion?” Yes, you could, but if your algorithm takes $n^2$ steps in the worst case scenario, then for some value of $n$, it will pass “$n$ times a billion”:

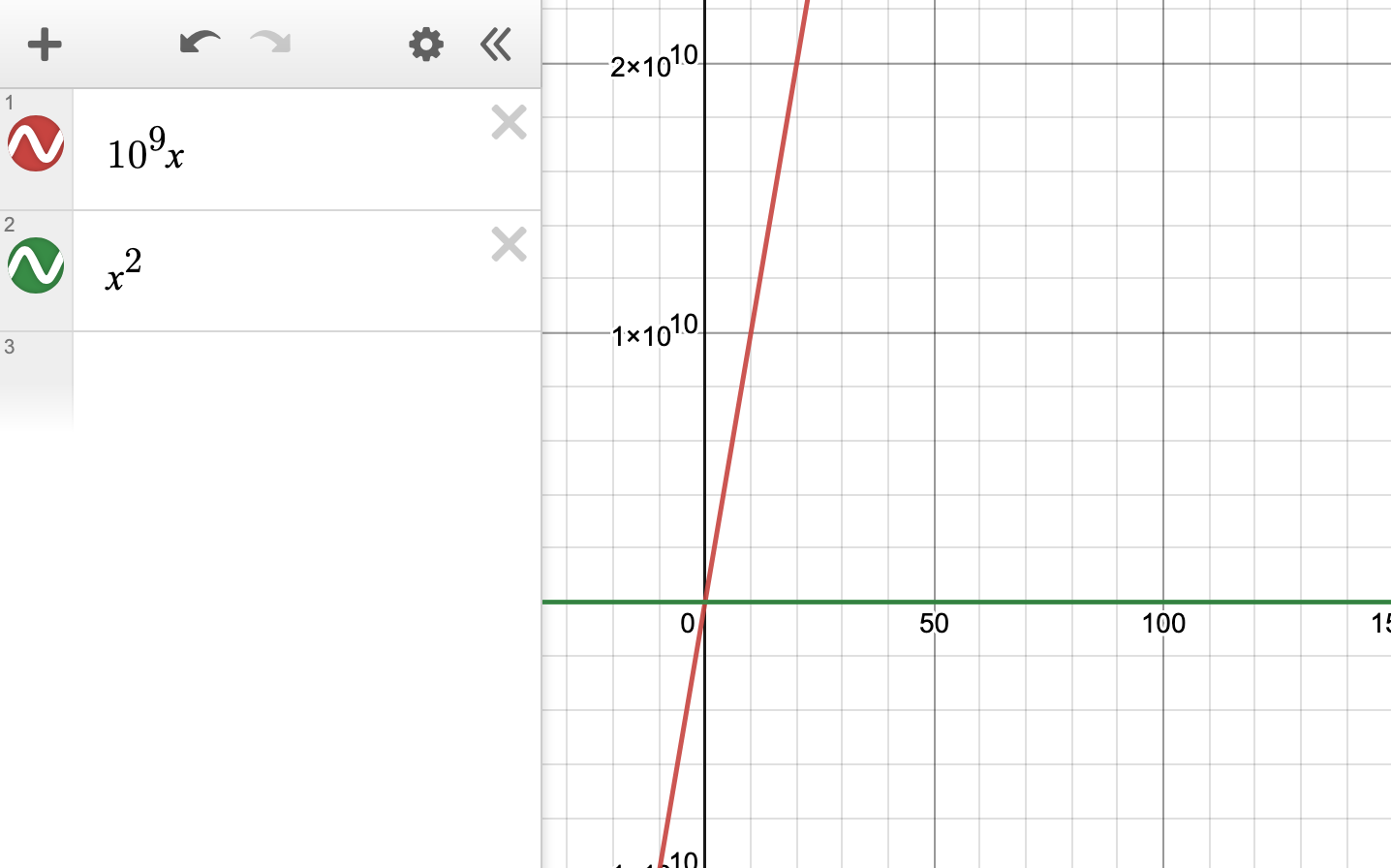
“Aha! I got you. See, $n$ times a billion is higher than your $n^2$!” Not so fast. What if we scale to, say, $10^{18}$?”

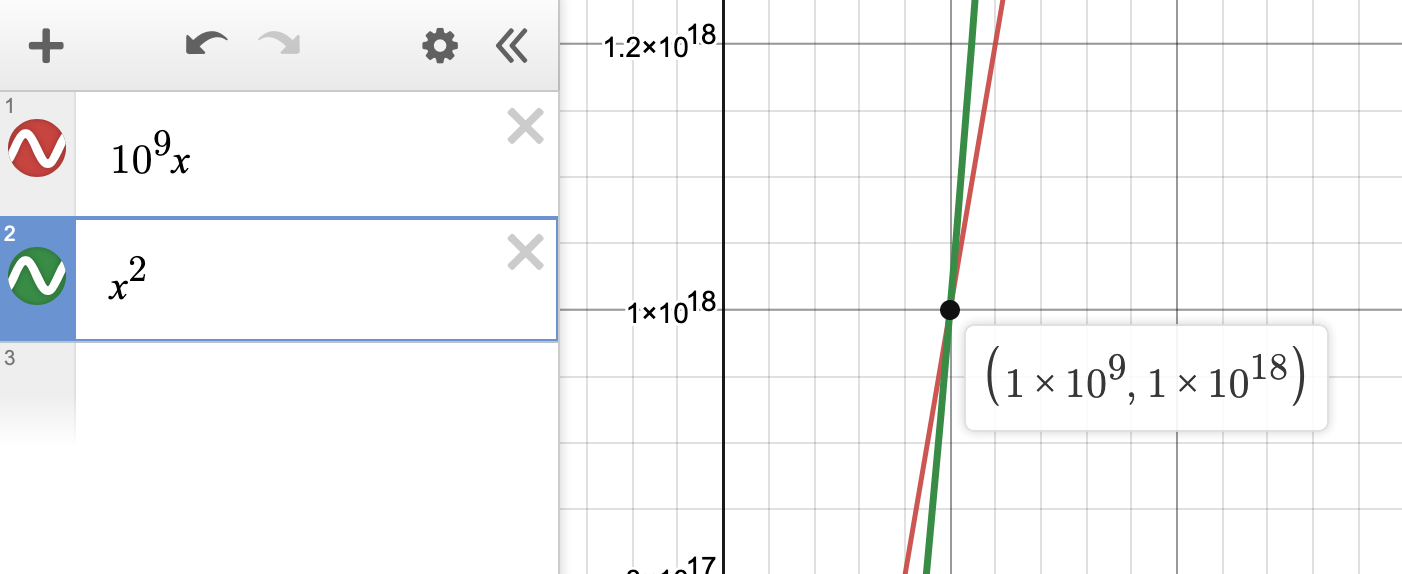
Since the function $n^2$ grows faster than $n$, there is a point where the algorithm could hypothetically take longer than “a billion times $n$ steps”. Since the upper bound is all that really matters here, programmers use this to denote the upper bound of an algorithm’s runtime. We call this “time complexity”.

Appendix #

Unverified Python #

Here’s the algorithm mentioned above in Python. No guarantees of correctness, lol.

A = [1, 3, 2]
R = []

while A:
	minimum = A[0]
	for N in A:
		minimum = min(minimum, N)
	R.append(minimum)
	A.remove(minimum)

Some considerations:

• There is already a more efficient sorting algorithm implemented in Python, callable with sort().
• This removes elements from the list A. If you wish to retain elements, a copy would need to be made.

Loosey-Goosey Proof of Correctness #

Prove: Given an arbitrary array of numbers $A$, the algorithm $B$ produces an array $R$ of numbers meeting the partial order $\leq$.

1. That the loop terminates is trivial. For each iteration of array $A$, at least one element is removed. Since the outermost loop terminates when $

   A

   = 0$ , the loop will terminate after $

   A

   $ iterations.

2. That the algorithm is correct for iteration $i =0$ is also trivial. The sorted order of the first zero elements of $A$ is the empty set, $\emptyset$.
3. Take some iteration $i$. Assume $R_i$ to be the first $i$ sorted elements of $A$, and $A_i$, the value of $A$ at iteration $i$, to be equal to $A \setminus R_i$.
   1. The innermost loop finds the minimum element of $A_i$, and removes it from $A_i$ to produce $A_{i+1}$.
   2. $R_{i+1}$ is now equal to the sorted version of the first $i+1$ sorted elements of $A$.